

Hence, there is no AAA criterion for congruence. Two triangles with equal corresponding angles may not be congruent to each other because one triangle might be an enlarged copy of the other.They are SSS, SAS, ASA, AAS, and RHS criteria. There are five conditions to determine if two triangles are congruent.Two triangles are congruent if the six parts (3 sides and 3 angles) of one triangle are equal to the corresponding six parts of the other triangle.If Δ ABC ≅ ΔXYZ under RHS criterion, then the third side (AB) and the other two angles of Δ ABC are bound to be equal to the corresponding side (XY) and angles of ΔXYZ. Under this criterion, two triangles are congruent, if the hypotenuse and side of one right-angled triangle are equal to the hypotenuse and the corresponding side of another right-angled triangle. RHS criterion stands for right angle-hypotenuse-side congruence criterion.
If ΔABC ≅ ΔXYZ under AAS criterion, then the third angle (∠ABC) and the other two sides (AC and BC) of Δ ABC are bound to be equal to the corresponding angle (∠XYZ) and the sides (XZ and YZ) of ΔXYZ. Under the AAS criterion, two triangles are congruent if any two angles and the non-included side of one triangle are equal to the corresponding angles and the non-included side of the other triangle. AAS Criterion for CongruenceĪAS criterion stands for Angle-Angle-Side criterion. If Δ ABC ≅ ΔXYZ under ASA criterion, then the third angle (∠BAC) and the other two sides of Δ ABC are bound to be equal to the corresponding angle (∠YXZ) and the sides of ΔXYZ. Under the ASA criterion, two triangles are congruent if any two angles and the side included between them of one triangle are equal to the corresponding angles and the included side of the other triangle.

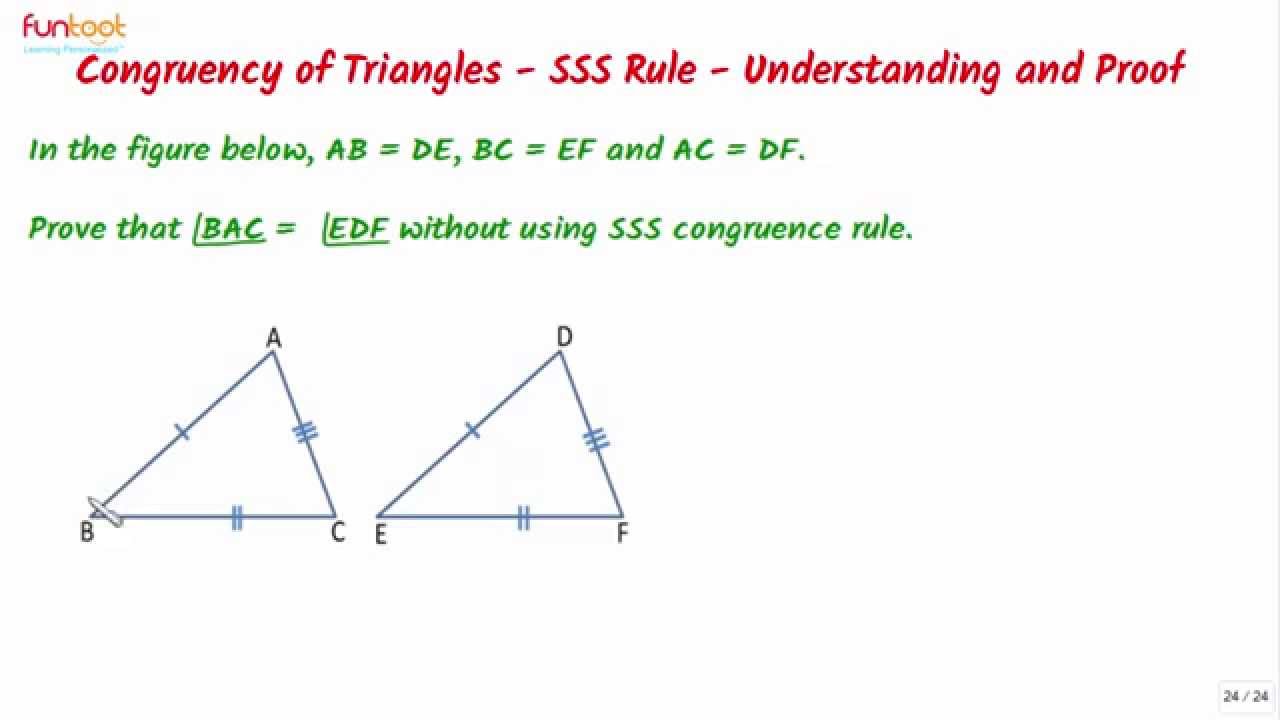
ASA Criterion for CongruenceĪSA criterion stands for Angle-Side-Angle criterion. If Δ ABC ≅ ΔXYZ under SAS criterion, then the third side (AB) and the other two angles of Δ ABC are bound to be equal to the corresponding side (XY) and the angles of ΔXYZ. Under this criterion, two triangles are congruent if the two sides and the included angle of one triangle are equal to the corresponding sides and the included angle of the other triangle. SAS criterion stands for Side-Angle-Side criterion. If Δ BAC ≅ ΔXYZ under SSS criterion, then the three angles of ΔBAC are bound to be equal to the corresponding angles of ΔXYZ. Under this criterion, two triangles are congruent if three sides of a triangle are equal to the corresponding sides of the other triangle. SSS criterion stands for Side-Side-Side criterion. They are SSS, SAS, ASA, AAS, and RHS congruence properties. Based on studies and experiments, there are 5 conditions for two triangles to be congruent. Necessarily, not all the six corresponding elements of both the triangles must be found to determine that they are congruent. Two triangles are said to be congruent if they are of the same size and same shape. Thus on identifying the corresponding parts of the given triangles, we can confirm that Δ ABC ≅ ΔPQR. In that case, we need to identify the six parts of a triangle and their corresponding parts in the other triangle. When we rotate, reflect, and/ or translate a triangle, its position or appearance seems to be different. Both the triangles under consideration should superimpose on each other. The two triangles need to be of the same size and shape to be congruent. In Δ PQR and ΔXYZ, as shown below, we can identify that PQ = XY, PR = XZ, and QR = YZ and ∠P = ∠X, ∠Q = ∠Y and ∠R = ∠Z. If the three angles and the three sides of a triangle are equal to the corresponding angles and the corresponding sides of another triangle, then both the triangles are said to be congruent.


 0 kommentar(er)
0 kommentar(er)
